北方酱Hoppou~

# 15. Scikit-learn

# 1. 简介

  1. Scikit-learn（曾叫做 scikits.learn 还叫做 sklearn）是用于 Python 编程语言的自由软件机器学习库。它的特征是具有各种分类、回归和聚类算法，包括支持向量机、随机森林、梯度提升、k-平均聚类和 DBSCAN，它被设计协同于 Python 数值和科学库 NumPy 和 SciPy。

  2. 安装

    # 必须用 scikit-learn，用 sklearn 安装的是错误的
pip install scikit-learn
    1
    2

  3. 官方 中文文档🔗 (opens new window)

  4. 聚类算法对比🔗 (opens new window)

    图 1

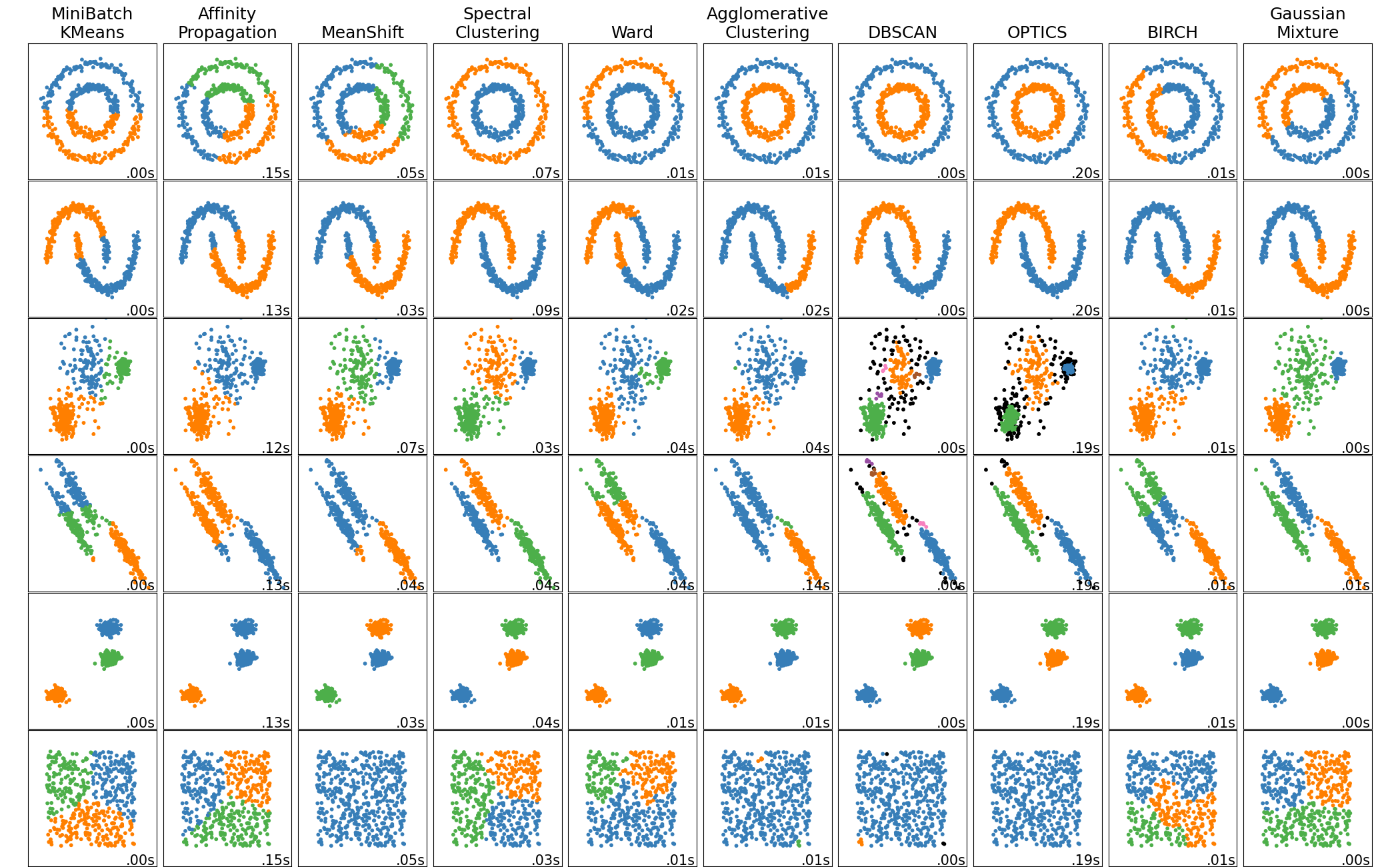
# 2. 常用函数

# 2.1. 归一化

  1. z-score 归一化

    from sklearn.preprocessing import StandardScaler
import numpy as np

data = np.array([1, 2, 3, 4, 5])  # [1 2 3 4 5]
scaler = StandardScaler()  # 创建缩放器
data = np.reshape(data, (-1, 1))  # 数据变成 n*1 [[1], [2], [3], [4], [5]]
# 需要输入列数据，
data = scaler.fit_transform(data)  # [[-1.41421356] [-0.70710678] [ 0.        ] [ 0.70710678] [ 1.41421356]]
print(scaler.mean_)  # [3.]
    1
    2
    3
    4
    5
    6
    7
    8
    9

  2. min_max 归一化

    from sklearn.preprocessing import MinMaxScaler
import numpy as np

# 归一化范围 0~1
data = np.array([1, 2, 3, 4, 5])    # [1 2 3 4 5]
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建缩放器，范围 0~1
data = np.reshape(data, (-1, 1))  # 数据变成 n*1 [[1], [2], [3], [4], [5]]
data = scaler.fit_transform(data)  # [[0.  ], [0.25], [0.5 ], [0.75], [1.  ]]
    1
    2
    3
    4
    5
    6
    7
    8

  3. 归一化还原

    # 接续上述代码
data = scaler.inverse_transform(data)   # [[1.], [2.], [3.], [4.], [5.]]
    1
    2

# 2.2. 分配训练集和测试集

  1. train_test_split

    from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.1, random_state=42)
# x_data: 要划分的样本特征集
# y_data: 要划分的样本结果
# test_size: 样本占比，如果是整数的话就是样本的数量
# random_state: 随机数的种子
    1
    2
    3
    4
    5
    6
    7

# 3. 层次聚类 Hierarchical clustering

  1. 使用 sklearn 中的 AgglomerativeClustering，其过程为

    1. 将每一个元素定为一类
    2. 每一轮都合并指定距离最小的一类
    3. 直到所有的元素都归为同一类

  2. 聚类参数

    参数 默认值 简介
    n_clusters 2 聚类个数
    affinity euclidean 距离的类型
    memory none 用于缓存输出的结果
    connectivity none 连接矩阵
    compute_full_tree auto 是否生成完整的树
    linkage ward 指定距离
    distance_threshold none 距离阈值
    1. compute_full_tree：为auto时在满足 n_clusters 时训练停止，为true时会继续训练从而生成一颗完整的树
    2. 指定距离：
      • ward：最小化正在合并的集群的方差
      • complete：使用两个集合的每个观测距离的平均值。
      • average：使用两个集合的所有观测值之间的最大距离。
      • single：两个集合的所有观测值之间的距离的最小值。
    3. distance_threshold：链接距离阈值，超过该阈值，集群将不被合并。如果该值不为 0，n_clusters 必须为 0，compute_full_tree 必须为 true
    from sklearn.cluster import AgglomerativeClustering

zones = 10  # 聚类个数，即聚成几类
data = pd.read_csv()    # 聚类数据，比如 Pearson 相关性系数

# 聚类器（聚类个数，聚类方法）
sk = AgglomerativeClustering(zones, linkage='ward')
# 聚类
sk.fit(data)

# 输出结果
out = sk.labels_    # 每个数据的类别编号
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12

  3. 参数

    linkage 中文名 说明
    ward 单链接 最小距离
    complete 全链接 最大距离
    average 均链接 平均距离

  4. 示例：以相关性系数作为聚类依据，其数据格式如下

    Pear a b c d
    a 1 0.53 0.67 0.98
    b 0.53 1 0.89 0.21
    c 0.67 0.89 1 0.74
    d 0.98 0.21 0.74 1
    import pandas as pd
from sklearn.cluster import AgglomerativeClustering

data = pd.DataFrame({'a': [1.0, 0.53, 0.67, 0.98],
                    'b': [0.53, 1.0, 0.89, 0.21],
                    'c': [0.67, 0.89, 1.0, 0.74],
                    'd': [0.98, 0.21, 0.74, 1.0]},
                    index=list('abcd'))

# linkage：ward-单链接（最小距离），complete-全链接（最大距离），average-均链接（平均距离）
sk = AgglomerativeClustering(2, linkage='ward')  # 分 2 个类
sk.fit(data)
index = data.index  # [a,b,c,d]
# 分类结果
out = sk.labels_  # [1 0 0 1]
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15

    对应的结果：两个区域分别为 [a, d] 和 [b, c]

  5. 参考

# 4. k 均值聚类 k-means

# 4.1. K-Means 简介

  1. K-Means 原理：对于给定的样本集，按照样本之间的距离大小，将样本集划分为 K 个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大
  2. 传统 K-Means 流程
    1. 选择 k 值
    2. 随机选择 k 个初始化质心
    3. 计算样本到各个质心的距离，按照距离最小划分类别
    4. 重新选择质心，重复第 3 步骤
    5. 若质心向量不变则输出分区，负责重新选择质心
  3. K-Means++ 算法
    1. 质心优化：第一个质心随机选择，与当前质心距离较远的点被选择聚类中心的概率较大
  4. K-Means 距离计算优化 elkan
    1. 目的是减少不必要的距离计算
    2. 原理：三角形两边之和大于等于第三边，两边只差小于第三边
      1. 如果预先知道两个质心的距离 D(j1, j2), 若点 x 到满足 2D(x, j1) < D(x, j2), 则 D(x, j1) < D(x, j2)
      2. D(x, j1) ≥ max{0, D(x, j1)-D(j1, j2)}
    3. 样本稀疏的情况下不适用
  5. 大样本优化 Mini Batch K-Means
    1. 用样本中的一部分样本 (batch size) 来做传统的 K-Means
    2. 精度会有所下降，一般会多跑几次，选择最优

# 4.2. 源码

  1. 基于 sklearn 的 K-Means 算法

    from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 创建数据集
# x 为样本特征，y 为样本簇类别，1000 样本，每个样本两个特征
# 共 4 个簇，簇中心为 [1, 1], [1, -1], [-1, 1], [-1, -1], 簇方差为分别 [0.4, 0.4, 0.2, 0.2]
x, y = make_blobs(n_samples=1000, n_features=2, centers=[[1, 1], [1, -1], [-1, 1], [-1, -1]],
               cluster_std=[0.4, 0.4, 0.2, 0.2])

# plt.scatter(x[:, 0], x[:, 1], marker='o')
# plt.show()

# n_clusters: K 值
# max_iter: 最大迭代次数
# n_init: 用不同初始化之心运行算法的次数，默认 10. K 较大时可适当增大
# init: 初始值选择方式，随机选择'random', 优化过的'k-means++', 一般用默认的'k-means++'
# algorithm: 'auto', 'full', 'elkan'三种选择，一般用默认'auto'
# random_state: 用于随机产生中心的随机序列
y_pred = KMeans(n_clusters=4, random_state=2).fit_predict(x)
# 下面三行与上面这句等价
# km = KMeans(n_clusters=4, random_state=2)
# km.fit(x)
# y_pred = km.predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27

  2. 输出结果

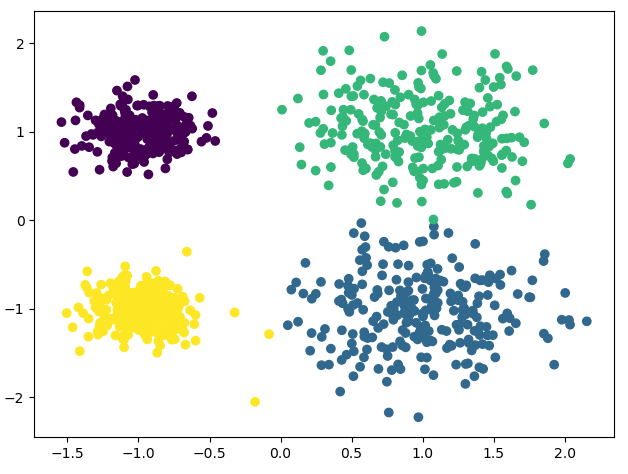
    k-means1

# 4.3. 参考

# 5. 随机森林 Random Forest

# 5.1. 简介

  1. 简介

    随机森林是由很多决策树构成的，不同决策树之间没有关联。当我们进行分类任务时，新的输入样本进入，就让森林中的每一棵决策树分别进行判断和分类，每个决策树会得到一个自己的分类结果，决策树的分类结果中哪一个分类最多，那么随机森林就会把这个结果当做最终的结果。

  2. 介绍参考 随机森林🔗 (opens new window)

  3. 应用场景：分类，回归，聚类，异常检测

# 6. SVM 支持向量机

# 6.1. 程序 1

  1. 程序 1 说明

    1. 程序主要功能为二维数据分成两类
    2. 数据类型（二维）：x 坐标，y 坐标，标签
    3. 输出：分类准确率，支持向量个数

  2. 程序 1 代码

    # 用 sklearn svm 训练 rbf
import os
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
import csv
from sklearn.model_selection import train_test_split, GridSearchCV
path1 = os.path.abspath('.')

# 加载数据
def load(name):
    file = np.loadtxt(open(name, 'rb'), delimiter=',')
    x = file[:, [0, 1]]
    y = file[:, 2]
    return x, y

if __name__ == "__main__":
    # 读取数据，针对二维线性不可分数据
    data, label = load('./data/train.csv')
    # 交叉验证 4:1
    x_train, x_test, y_train, y_test = train_test_split(data, label, test_size=.2, random_state=0)
    # 设置参数
    c = 5000  # 惩罚参数
    g = 0.5  # 核函数参数
    # 初始化模型参数
    clf = SVC(cache_size=200, class_weight=None, coef0=0.0, C=c, decision_function_shape='ovr',
            degree=3, gamma=g, kernel='rbf', max_iter=-1, probability=False,
            random_state=None, shrinking=True, tol=0.001, verbose=False)
    clf.fit(x_train, y_train)
    # 预测 data
    predict_list = clf.predict(x_test)
    # 预测精度
    precision = clf.score(x_test, y_test)
    print('第', i+1, '次 precision is : ', precision*100, "%")
    # 获取模型返回值
    n_Support_vector = clf.n_support_  # 支持向量个数
    print("支持向量个数为： ", n_Support_vector)
    Support_vector_index = clf.support_  # 支持向量索引
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39

# 6.2. 程序 2

  1. 程序 2 在程序 1 的基础上添加了画图功能

  2. 程序 2 代码

    # 用 sklearn svm 训练，画图
import os
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
import csv
from sklearn.model_selection import train_test_split
path1 = os.path.abspath('.')

# 加载数据
def load(name):
    file = np.loadtxt(open(name, 'rb'), delimiter=',')
    x = file[:, [0, 1]]
    y = file[:, 2]
    return x, y

# 用返回的参数绘制超平面
def plot_point(data, label, Support_vector_index, clf, title):
    for i in range(np.shape(data)[0]):
        if label[i] == 1:
            plt.scatter(data[i][0], data[i][1], c='b', s=20)
        else:
            plt.scatter(data[i][0], data[i][1], c='y', s=20)
    for j in Support_vector_index:
        plt.scatter(data[j][0], data[j][1], s=100, c='', alpha=0.5, linewidth=1, edgecolor='g')
    # 画超平面
    x_min, x_max = data[:, 0].min() - 0.01, data[:, 0].max() + 0.01
    y_min, y_max = data[:, 1].min() - 0.01, data[:, 1].max() + 0.01
    h = 0.001
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    z = clf.predict(np.c_[xx.ravel(), yy.ravel()])  # SVM 的分割超平面
    # Put the result into a color plot
    z = z.reshape(xx.shape)
    plt.contourf(xx, yy, z, cmap='hot', alpha=0.3)
    plt.title(title)
    plt.show()

if __name__ == "__main__":
    # 读取数据，针对二维线性不可分数据
    data, label = load('./data/train.csv')
    # 交叉验证
    x_train, x_test, y_train, y_test = train_test_split(data, label, test_size=.2, random_state=0)
    # 参数设置
    c = 1000
    g = 0.1
    # 初始化模型参数
    clf = SVC(cache_size=200, class_weight=None, coef0=0.0, C=c, decision_function_shape='ovr',
            degree=3, gamma=g, kernel='rbf', max_iter=-1, probability=False,
            random_state=None, shrinking=True, tol=0.001, verbose=False)
    clf.fit(x_train, y_train)
    # 预测 data
    predict_list = clf.predict(x_test)
    # 预测精度
    precision = clf.score(x_test, y_test)
    print('第', i+1, '次 precision is : ', precision*100, "%")
    # 获取模型返回值
    n_Support_vector = clf.n_support_  # 支持向量个数
    print("支持向量个数为： ", n_Support_vector)
    Support_vector_index = clf.support_  # 支持向量索引
    title = 'C=' + str(c) + ', gamma=' + str(g)
    # 画图
    plot_point(data, label, Support_vector_index, clf, title)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67

# 7. 谱聚类 Spectral Clustering

  1. 示例程序

    import numpy as np
from sklearn import datasets
from sklearn.cluster import SpectralClustering
import matplotlib.pyplot as plt

X, y = datasets.make_blobs(n_samples=500, n_features=3, centers=5, cluster_std=[0.4, 0.3, 0.4, 0.3, 0.4],
                        random_state=11)
# 分类数=5
y_pred = SpectralClustering(5).fit_predict(X)

fig = plt.figure()

ax = fig.add_subplot(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y_pred)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

plt.show()
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
lastUpdate: 3/30/2023, 2:14:30 PM

← 16. Tkinter →