# 14. Keras 学习笔记
# 1. 安装
pip 安装
# 安装 cpu 版的 tensorflow, 最新版本的 python 不一定支持,不建议 python 版本太新 pip install tensorflow # 或者安装 gpu 版的 tensorflow(需要 CUDA 支持) pip install tensorflow-gpu # 安装 keras pip install keras1
2
3
4
5
6
7使用 gpu 进行训练需要配置 cuda 环境,参考 CUDA 安装
使用 gpu 进行训练
# 在代码开头加入如下设置 import os os.environ["CUDA_VISIBLE_DEVICES"] = '0' # 使用 0 号 gpu1
2
3
4keras 结构
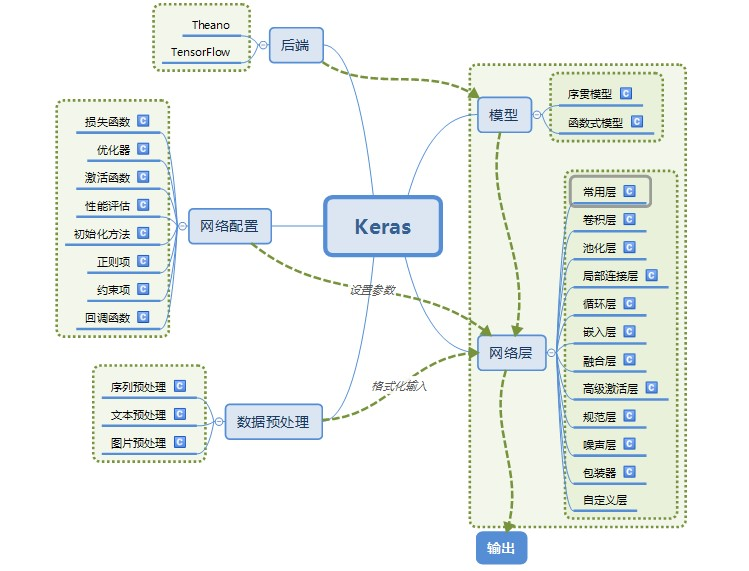
# 2. keras 层
# 2.1. 核心层
全连接层:神经网络中最常用的,实现对神经网络里的神经元激活
# units:全连接层输出的维度,即下一层神经元的个数 # activation:激活函数,默认使用 Relu # use_bias:是否使用 bias 偏置 Dense(units, activation='relu', use_base=True) # 作为输入层:输入为 60*1 维数据,激活函数 relu model.add(Dense(200, input_shape=(60,), activation='relu')) # 作为中间层(隐含层) model.add(Dense(200, activation='relu')) # 作为输出层,units = 输出维数 model.add(Dense(60))1
2
3
4
5
6
7
8
9
10
11
12
13激活层:对上一层的
# 激活函数,relu、tanh、sigmoid 等 Activation(activation)1
2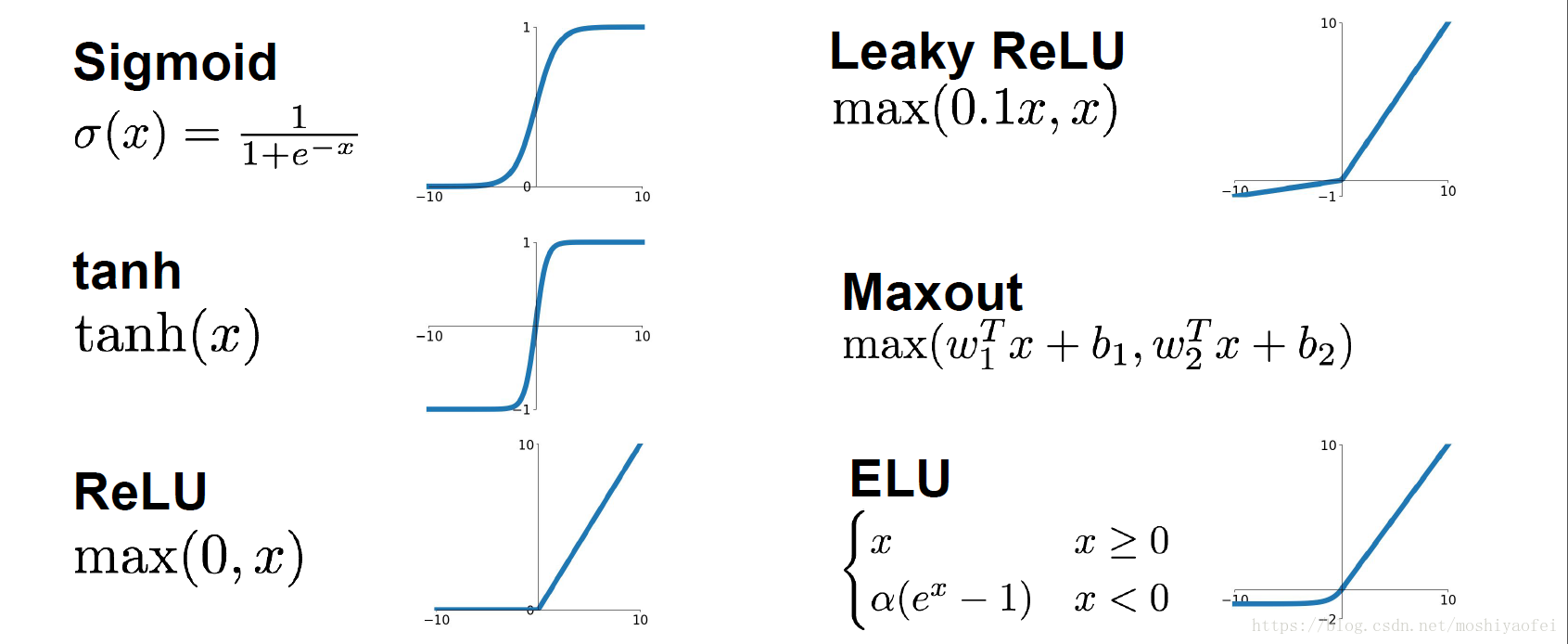
Dropout 层:对上一层的神经元随机选取一定比例的失活,不更新,但是权重仍然保留,防止过拟合
# rate:失活比例,0-1 浮点数 Droupout(rate)1
2Flatten 层:将一个维度大于或等于 3 的高维矩阵,“压扁”为一个二维矩阵。即保留第一个维度(如:batch 的个数),然后将剩下维度的值相乘作为“压扁”矩阵的第二个维度
Flatten()1Reshape 层:将输入的维度重构成特定的 shape
# target_shape:目标矩阵的维度,不包含 batch 样本数 Reshape(target_shape)1
2卷积层:卷积操作分为一维、二维、三维,分别为 Conv1D、Conv2D、Conv3D。一维卷积主要应用于以时间序列数据或文本数据,二维卷积通常应用于图像数据。由于这三种的使用和参数都基本相同,所以主要以处理图像数据的 Conv2D 进行说明
# filters:卷积核的个数 # kernel_size:卷积核的大小 # strides:步长,二维中默认为 (1,1),一维中默认为 1 # Padding:补“0”策略,‘valid’指卷积后的大小与原来的大小可以不同,‘same’指卷积后的大小与原来大小一致 Conv2D(filters, kernel_size, strides=(1,1), padding='valid')1
2
3
4
5池化层:与卷积层一样,最大统计量池化和平均统计量池化也有三种,分别为 MaxPooling1D、MaxPooling2D、MaxPooling3D 和 AveragePooling1D、AveragePooling2D、AveragePooling3D,由于使用和参数基本相同,所以主要以 MaxPooling2D 进行说明
# poll_size:长度为 2 的整数 tuple,表示在横向和纵向的下采样因子,一维则为纵向下采样因子 MaxPolling(poll_size=(2,2), strides=None, padding='valid') # 上面的代码表示1
2
3循环层:循环神经网络中的 RNN、LSTM 和 GRU 都继承本层,所以该父类的参数同样使用于对应的子类 SimpleRNN、LSTM 和 GRU
# retrun_sequences:控制返回类型,‘False’返回输出序列的最后一个输出,‘True’则返回整个序列 Recurrent(return_sequences=False)1
2嵌入层:该层只能用在模型的第一层,是将所有索引标号的稀疏矩阵映射到致密的低维矩阵。如我们对文本数据进行处理时,我们对每个词编号后,我们希望将词编号变成词向量就可以使用嵌入层
# input_dim:大或等于 0 的整数,字典长度,即输入数据最大下标+1 # output_dim:大于 0 的则行数,代表全连接嵌入的维度 # input_length:当输入序列的长度固定时,该值为其长度。如果要在该层后接 Flatten 层,然后接 Dense 层,则必须指定该参数,否则 Dense 层的输出维度无法自动推断 Embedding(input_dim, output_dim, input_length)1
2
3
4
# 2.2. 求解 compile
创建求解
model.compile(loss='mean_squared_error', # 损失函数 optimizer='adam', # 优化器 metrics=['accuracy']) # 准确率标准1
2
3损失函数 loss
函数 中文名 mean_squared_error 均方误差 mean_absolute_error 平均绝对误差 mean_absolute_percentage_error 平均绝对百分比误差 mean_squared_logarithmic_error 均方对数误差 squared_hinge 平方合页(铰链) hinge 合页(铰链) categorical_hinge 分类合页(铰链) logcosh 预测误差的双曲余弦的对数 categorical_crossentropy 分类交叉熵 优化器 optimizer
函数 备注 SGD 随机梯度下降 RMSprop RMSProp 优化器,MSProp 优化算法是 AdaGrad 算法的一种改进。将梯度除以最近幅度的移动平均值。 Adagrad Adagrad 是一种具有特定参数学习率的优化器,它根据参数在训练期间的更新频率进行自适应调整。 Adadelta Adadelta 是 Adagrad 的一个具有更强鲁棒性的的扩展版本 Adam Adam 本质上是 RMSProp 与动量 momentum 的结合 Adamax Adam 算法基于无穷范数(infinity norm)的变种 Nadam Nesterov 版本 Adam 优化器 评价函数 metrics:同损失函数相似,但是评价函数不会用于训练
参考链接
# 2.3. 训练 fit
创建训练
# 模型训练 # x_train: 训练集输入 # y_train: 训练集输出 # validation_split: 交叉验证 # batch_size: 每组训练 32 个数据,60000 数据就要训练 60000/32=1875 组 # epochs: 训练 5 回合 # verbose: 1-训练过程可视;0-训练结果不可视 model.fit(x_train, y_train, validation_split=0.5, batch_size=100, epochs=100, verbose=1) # 如果有专门的验证集 # x_test: 验证集输入 # y_test: 验证集输出 model.fit(x_train, y_train, validation_data=[x_test, y_test], batch_size=100, epochs=100, verbose=1)1
2
3
4
5
6
7
8
9
10
11
12参数设置
参数 配置 备注 validation_split 0~1 默认不进行交叉验证,交叉验证比例:0.1 表示每次保留 10%数据进行验证 batch_size 整数 表示每次进行训练的数据个数,数字越大内存(或显存)占用越大 epochs 整数 最大训练回合数,如果没有设置提前截至条件则就是训练回合数 verbose 0/1,默认 0 1-训练过程可视;0-训练结果不可视 参数关系
每个 epoch 训练的组数 = \frac{x\_train.size() * (1-validation\_split)}{batch\_size}早停法
from keras import callbacks # monitor: loss/accuracy/val_loss/val_accuracy # patience: callback = callbacks.EarlyStopping(monitor='loss', patience=20) model.fit(x_train, y_train, validation_split=0.05, batch_size=500, epochs=300, verbose=1, callbacks=[callback])1
2
3
4
5
6
# 2.4. 模型保存与加载
保存模型
model.save('./model/model_name.h5')1加载模型
from keras.models import load_model model = load_model('./model/model_name.h5') # 还可以继续训练,参数与训练时的参数相同 model.fit(x_train, y_train, ...)1
2
3
4
5
6模型使用
# 模型输出 y_pre = model.predict(x_input)1
2
# 3. 模型搭建
# 3.1. 多层感知机(全链接/DNN) MLP
模型搭建
def build_model(self): # 创建模型 units = 500 # 神经元 model = Sequential() # 输入层 model.add(Dense(1000, input_shape=(60,), activation='relu')) # 隐含层 model.add(Dense(4 * units, activation='relu')) model.add(Dropout(0.2)) model.add(Dense(2 * units, activation='relu')) model.add(Dropout(0.2)) model.add(Dense(units, activation='tanh')) model.add(Dropout(0.1)) # 输出层 model.add(Dense(60)) # 显示模型 model.summary() self.model = model # 在类中时将模型赋给类变量1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19模型训练
def train(self): # 模型训练 model = self.model model.compile(loss='mse', # 损失函数 optimizer='adam', # 优化器 metrics=['accuracy', 'mae']) # 准确率标准 x_train, y_train = self.x_data, self.y_data # 训练模型 callback = callbacks.EarlyStopping(monitor='accuracy', patience=5) model.fit(x_train, y_train, validation_split=0.05, batch_size=500, epochs=300, verbose=1, callbacks=[callback]) # 保存训练过程 df_his = pd.DataFrame({ 'loss': model.history.history['loss'], 'acc': model.history.history['accuracy'], 'val_loss': model.history.history['val_loss'], 'val_acc': model.history.history['val_accuracy'] }) df_his.to_csv('../data/model_his.csv', index=False) # 保存模型 model.save(self.model_name) print('保存模型:', self.model_name)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 3.2. 手写数字识别,原文链接🔗 (opens new window)
加载数据,第一次运行会联网下载数据(可复制运行)
from keras.datasets import mnist import matplotlib.pyplot as plt # (训练集输入,训练集输出), (测试集输入,测试集输出) = 从 mnist 中加载数据集 (trainX, trainY), (testX, testY) = mnist.load_data() # 训练集 60000 个 28*28 像素个手写数字图片 print('Train: X=%s, Y=%s' % (trainX.shape, trainY.shape)) # Train: X=(60000, 28, 28), Y=(60000,) # 测试集 10000 个 28*28 像素个手写数字图片 print('Test: X=%s, Y=%s' % (testX.shape, testY.shape)) # Test: X=(10000, 28, 28), Y=(10000,) # 画出一些图 for i in range(9): plt.subplot(330 + 1 + i) plt.imshow(trainX[i]) plt.show()1
2
3
4
5
6
7
8
9
10
11
12
13
14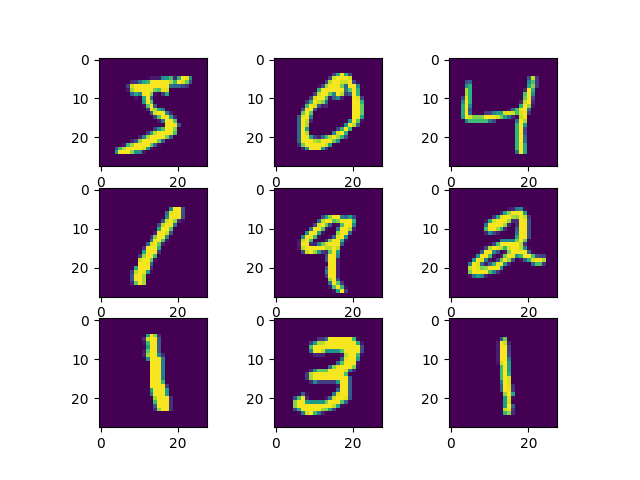
神经网络模型创建 & 训练(可复制运行)
from keras.datasets import mnist from keras import Sequential from keras.layers import Dense, Dropout, Activation, Flatten # 常用层 from keras.layers import Conv2D, MaxPool2D # 卷积层,池化层 from keras.utils import np_utils # (训练集输入,训练集输出), (测试集输入,测试集输出) = 从 mnist 中加载数据集 (trainX, trainY), (testX, testY) = mnist.load_data() # 数据集从形状(n,宽度,高度)转换为(n,宽度,高度,深度) X_train = trainX.reshape(trainX.shape[0], 28, 28, 1) X_test = testX.reshape(testX.shape[0], 28, 28, 1) print(X_train.shape) # (60000, 28, 28, 1) # 将 1 维类数组转换为 10 维类矩阵 Y_train = np_utils.to_categorical(trainY, 10) Y_test = np_utils.to_categorical(testY, 10) print(Y_train.shape) # (60000, 10), 除了对应位是 1 以外都是 0 # 模型结构 model = Sequential() # 创建一个序列 # 卷积层:32 个卷积核,卷积核 3*3, 激活函数 relu, 模型输入 (28, 28, 1) model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(Conv2D(32, kernel_size=(3, 3), activation='relu')) # 第二层卷积层 model.add(MaxPool2D(pool_size=(2, 2))) # 池化层 model.add(Dropout(0.25)) # Dropout 层 model.add(Flatten()) # Flatten 层:将高位矩阵压缩成 2 维矩阵 model.add(Dense(128, activation='relu')) # 中间层:全链接,输出维度 (128) model.add(Dropout(0.5)) # Dropout 层 model.add(Dense(10, activation='softmax')) # 输出层:全链接,输出维度 (10) model.summary() # 打印模型信息 model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 模型训练 # X_train: 训练集输入 # Y_train: 训练集输出 # batch_size: 每组训练 32 个数据,60000 数据就要训练 60000/32=1875 组 # epochs: 训练 5 回合 # verbose: 1-训练过程可视;0-训练结果不可视 model.fit(X_train, Y_train, batch_size=32, epochs=5, verbose=1) # 模型评估 # X_test: 测试集输入 # Y_test: 测试集输出 # batch_size: 默认 32 score = model.evaluate(X_test, Y_test, verbose=0) print(score)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51模型信息,model.summary() 打印结果
Model: "sequential" _________________________________________________________________ # 层 输出维度 参数个数 Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 26, 26, 32) 320 _________________________________________________________________ conv2d_1 (Conv2D) (None, 24, 24, 32) 9248 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 12, 12, 32) 0 _________________________________________________________________ dropout (Dropout) (None, 12, 12, 32) 0 _________________________________________________________________ flatten (Flatten) (None, 4608) 0 _________________________________________________________________ dense (Dense) (None, 128) 589952 _________________________________________________________________ dropout_1 (Dropout) (None, 128) 0 _________________________________________________________________ dense_1 (Dense) (None, 10) 1290 ================================================================= Total params: 600,810 # 总参数个数 Trainable params: 600,810 # 可训练参数 Non-trainable params: 0 # 不可训练参数 _________________________________________________________________1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26模型训练信息
Epoch 1/5 # 第 1 回合 # 训练集 60000, 32 个数据为一组训练,训练 60000/32=1875 组;回合耗时,每组耗时;损失;精度 1875/1875 [==============================] - 55s 29ms/step - loss: 0.4725 - accuracy: 0.8922 Epoch 2/5 # 第 2 回合 1875/1875 [==============================] - 64s 34ms/step - loss: 0.1421 - accuracy: 0.9591 Epoch 3/5 # 第 3 回合 1875/1875 [==============================] - 62s 33ms/step - loss: 0.1103 - accuracy: 0.9685 Epoch 4/5 # 第 4 回合 1875/1875 [==============================] - 65s 35ms/step - loss: 0.0964 - accuracy: 0.9719 Epoch 5/5 # 第 5 回合 1875/1875 [==============================] - 61s 33ms/step - loss: 0.0841 - accuracy: 0.97491
2
3
4
5
6
7
8
9
10
11
# 3.3. 长短期记忆 LSTM
单层 lstm 预测模型
# x_train 训练集输入 # x_train.shape[0] 表示 x_train 有多少条 # x_train.shape[1] 表示 x_train 每条数据有几个值 x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1)) # x_test 测试集输入 x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1)) print(x_train.shape) # 模型结构 model = Sequential() # 定义 LSTM 模型,第一个隐藏层含有 100 个神经元 model.add(LSTM(100, input_shape=(x_train.shape[1], x_train.shape[2]))) model.add(Dropout(0.25)) # 暂时从网络中移除神经网络中的单元 model.add(Dense(1)) # 输出维数 model.add(Activation('relu')) # 激活函数 # 使用均方差损失函数,优化器 Adam,评估标准 model.compile(loss=losses.mean_squared_error, # 损失函数 optimizer='adam', # 优化器 metrics=['mae']) # 评估标准 # 模型将会进行 30 个 epochs(回合)的训练,每个回合将数据分成 batch=100 的组进行训练 # 比如有 1000 条训练数据,batch_size=100 表示将 1000 条数据分成 10 组,每组 100 条数据,重复进行 epochs 次训练 history = model.fit(x_train, y_train, epochs=30, batch_size=100, validation_data=(x_test, y_test), # 验证集 callbacks=[EarlyStopping(monitor='val_loss', patience=10)], # 当被检测值不再提升,提前结束训练 verbose=1, # 日志显示(默认 1): 0-不在标准输出流输出日志信息;1-输出进度条记录;2-每个 epoch 输出一行记录 shuffle=True) # shuffle=False 不打乱数据顺序,一般设置为 True 训练结果会好一些 model.summary() # 打印模型信息 # 做出预测 test_predict = model.predict(x_test) # 预测值求逆 test_predict = scaler.inverse_transform(test_predict) # 真实值求逆 y_test = scaler.inverse_transform(y_test)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36多层 lstm 预测模型
# 创建神经网络 def build_model(x_train, y_train): # 模型结构 model = Sequential() # 定义 LSTM 模型 model.add(LSTM(100, input_shape=(x_train.shape[1], x_train.shape[2]), return_sequences=True)) # 第一层 lstm model.add(LSTM(60, return_sequences=False)) # 第二层 lstm model.add(Dropout(0.2)) # 暂时从网络中移除神经网络中的单元 model.add(Dense(1)) # 输出维数 model.add(Activation('relu')) # 使用均方差损失函数,优化器 Adam,评估标准 model.compile(loss=losses.mean_squared_error, # 损失函数 optimizer='adam', # 优化器 metrics=['mae']) # 评估标准 model.summary() return model1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19attention-lstm
# 安装 attention 包 pip install attention1
2# 创建神经网络 def build_model(x_train): # 模型结构 model = Sequential() # 定义 LSTM 模型 model.add(LSTM(100, input_shape=(x_train.shape[1], x_train.shape[2]), return_sequences=True)) # 第一层 lstm model.add(LSTM(100, return_sequences=True)) # 第二层 lstm model.add(Attention()) # attention 层 model.add(Dropout(0.1)) # 暂时从网络中移除神经网络中的单元 model.add(Dense(1)) # 输出维数 model.add(Activation('relu')) # 激活函数 # 使用均方差损失函数,优化器 Adam,评估标准 model.compile(loss=losses.mean_squared_error, # 损失函数 optimizer='adam', # 优化器 metrics=['mae']) # 评估标准 model.summary() # 显示模型信息 return model1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20训练结果
history 备注 loss 训练集损失(根据设置的损失函数) mae 训练集平均绝对误差 acc 训练集准确率(用于分类问题) val_loss 验证集损失(根据设置的损失函数) val_mae 验证集平均绝对误差 val_acc 验证集准确率(用于分类问题)
